Table des matières
Dans cette publication, nous examinerons ce qu'est une combinaison linéaire de chaînes, des chaînes linéairement dépendantes et indépendantes. Nous donnerons également des exemples pour une meilleure compréhension du matériel théorique.
Définition d'une combinaison linéaire de chaînes
Combinaison linéaire (LK) terme s1Avec2, …, sn matrice A appelé une expression de la forme suivante :
αs1 + αs2 + … + αsn
Si tous les coefficients αi sont égaux à zéro, donc LC est insignifiant. En d'autres termes, la combinaison linéaire triviale est égale à la ligne zéro.
Par exemple : 0 · s1 + 0 · s2 + 0 · s3
Ainsi, si au moins un des coefficients αi n'est pas égal à zéro, alors LC est non trivial.
Par exemple : 0 · s1 + 2 · s2 + 0 · s3
Lignes linéairement dépendantes et indépendantes
Le système de chaîne est linéairement dépendant (LZ) s'il existe une combinaison linéaire non triviale d'entre eux, qui est égale à la ligne zéro.
Il s'ensuit donc qu'un LC non trivial peut dans certains cas être égal à la chaîne zéro.
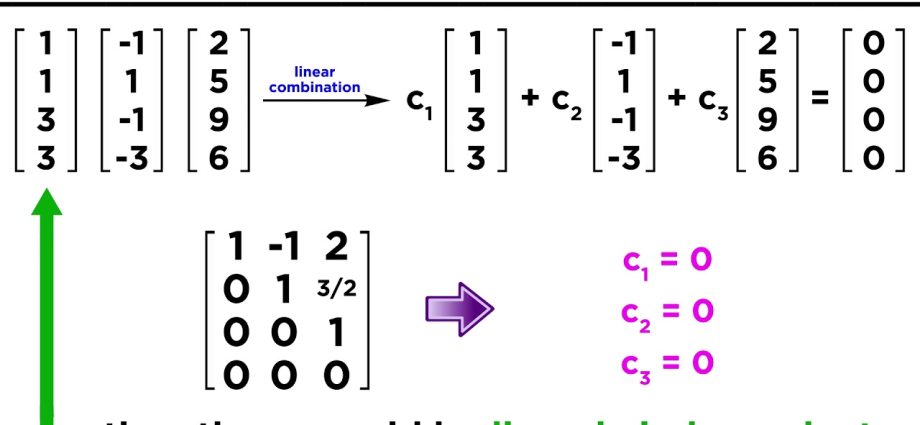
Le système de chaîne est linéairement indépendant (LNZ) si seul le LC trivial est égal à la chaîne nulle.
Notes:
- Dans une matrice carrée, le système de lignes est un LZ uniquement si le déterminant de cette matrice est nul (le = 0).
- Dans une matrice carrée, le système de lignes est un LIS uniquement si le déterminant de cette matrice n'est pas égal à zéro (le ≠ 0).
Exemple de problème
Voyons si le système de chaîne est
Décision:
1. Tout d'abord, faisons un LC.
α1{3 4} + un2{9}.
2. Découvrons maintenant quelles valeurs devraient prendre α1 и α2de sorte que la combinaison linéaire soit égale à la chaîne nulle.
α1{3 4} + un2{9 12} = {0 0}.
3. Faisons un système d'équations :
![]()
4. Divisez la première équation par trois, la seconde par quatre :
![]()
5. La solution de ce système est toute α1 и α2, Avec α1 = -3a2.
Par exemple, si α2 = 2puis α1 = -6. Nous substituons ces valeurs dans le système d'équations ci-dessus et obtenons:
![]()
Réponse donc les lignes s1 и s2 linéairement dépendant.